VITEEE 2018 :: Mathematics :: General questions

• Mathematics - General questions

If the equations x + ay - z = 0, 2x - y + az = 0, ax + y + 2z = 0 have non-trivial solutions, then a =

Answer:

Explanation:

$\begin{vmatrix}1 & a & -1 \\2 & -1 & a\\ a & 1& 2\end{vmatrix} = 0$

Applying R₂→ R₂ - 2R₁ and R₃ → R₃ - aR₁, we get

$\begin{vmatrix}1 & a & -1 \\0 & -1-2a & a+2\\ 0 & 1-a^{2}& 2+a\end{vmatrix} = 0$

Expanding along C₁, we get

$(a + 2) (a^{2} - 2a - 2) = 0\Rightarrow  a= - 2, 1\pm \sqrt{3}$

The value of the determinant Δ = $\begin{vmatrix}1 & 4& 3 \\0 & 12 & 9\\1 & 2 & 2 \end{vmatrix}$ is

Answer:

Explanation:

Δ = $\begin{vmatrix}1 & 4& 3 \\0 & 12 & 9\\1 & 2 & 2 \end{vmatrix}$

=  1(12 x 2 -2 x 9)-4 (0 x 2 - 1 x 9) + 3(0x 2 - 1 x12) = 1(24 - 18) - 4(0 - 9) + 3(0 - 12)

= 6 +36 - 36 = 6

A signal which can be green or red with probability 4/5 and 1/ 5 respectively, is received by station A and then transmitted to station B. The probability of each station receiving the signal correctly is 3/4. If the signal received at station B is given, then the probability that the original signal is green, is

Answer:

Explanation:

From the tree diagram, it follows that

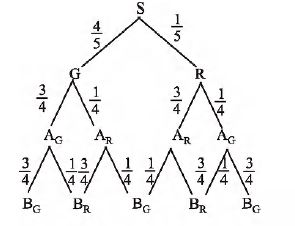
$P(B_{G}) = \frac{46}{80}$, $P(G) = \frac{4}{5}$

$P(B_{G}/G) = \frac{10}{16}$ = $\frac{5}{8}$

$\therefore P(B_{G}\cap G) = \frac{5}{8}\times\frac{4}{5}$ = $\frac{1}{2}$

$\left[\because P(B_{G}\cap G) = P\left(\frac{B_{G}}{G}\times P(G)\right)\right]$

Now , P(G/B_G)

$\frac{P(B_{G}\cap G)}{P(B_{G})}=\frac{1}{2}\times\frac{80}{40} = \frac{20}{23}$

 The area of the region bounded by the curve x = 2y + 3 and lines y = 1 and y = -1 is

Answer:

Explanation:

We have x= 2y + 3, a straight line

Required area =  Area of shaded region

$\int_{-1}^{1} (2y + 3)dy=\left[y^{2}+3y\right]$¹_-1 = 6 sq. units

The value of c in Rolle's Theorem for the function

f(x) = e^x sin x, x Ε [0, π] is

Answer:

Explanation:

Since Rolle's theorem is satisfied

.'. f'(c) = 0  →  e^c sin c + cos e^c = 0

→ e^c { sin c +cos c} = 0

.'. sin c + cos c = 0   ($\because e^{c}\neq0$)

→ tan c = -1 → c = tan^-1(-1) = $\pi-\frac{\pi}{4}$ = $\frac{3\pi}{4}$

• Mathematics - General questions